If we plot 4000 points on the line segment from (-1, 0) to (0, 1), and transform each of them with $M = \begin{bmatrix}2 & 3 &4\\-1 & 0 & 0\\2&2&1\end{bmatrix}$, we get an initially surprising result:
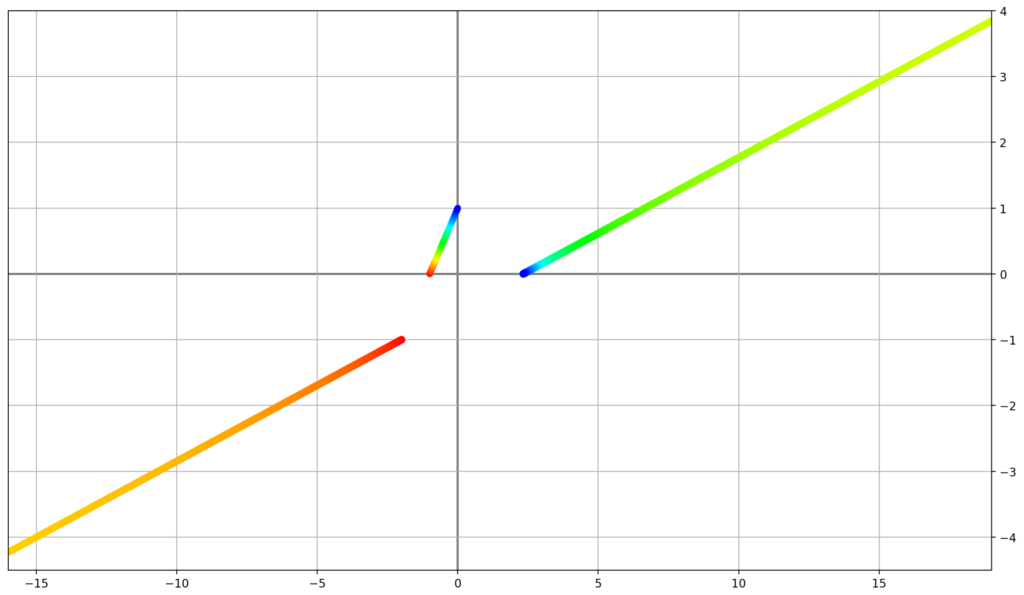
As we can see, something strange happens in the yellow region of the points. While the red-to-orange points get transformed to a top right to bottom left diagonal, some yellow point we transform jumps from the bottom left to the top right, and subsequent points continue to get transformed along that line.
What’s happening here is that $M$ happens to transform a yellow point onto a point at infinity. Below, we can see this visualised on the projective unit sphere model.
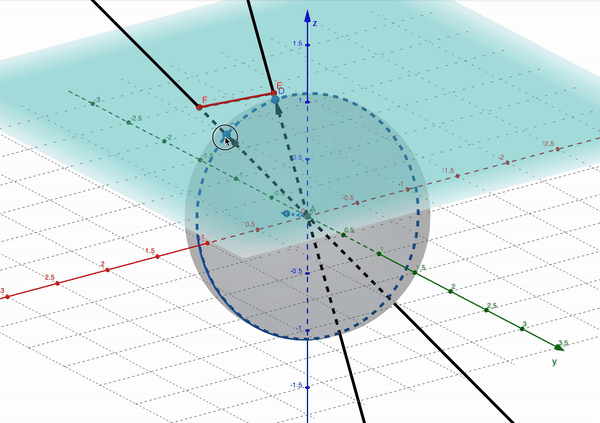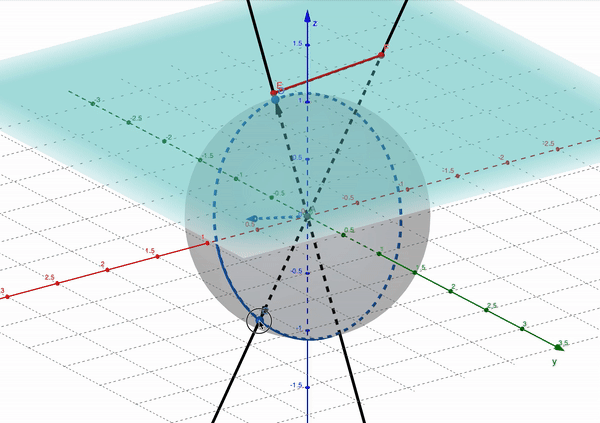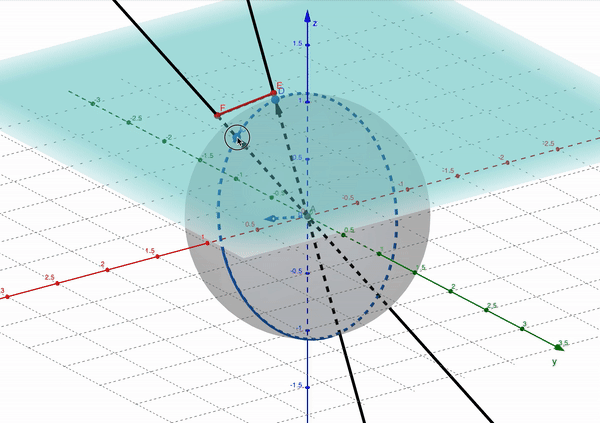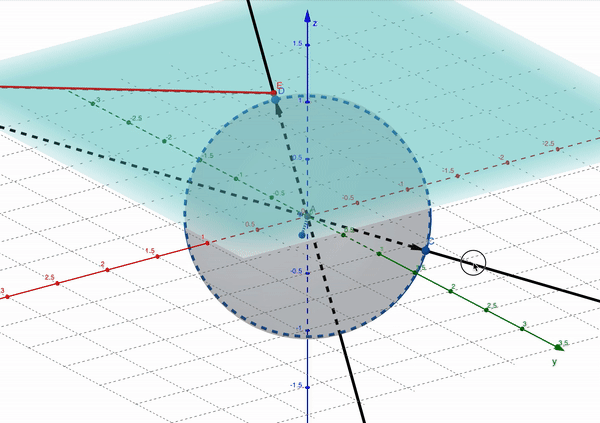
Notice how the red segment $\overleftrightarrow{EF}$ gets longer and longer as the line through the origin that generates point $E$ on the projective plane approaches a right angle with the $z$ axis, and then “jumps” over to reappear from the other side.
Leave a Reply