Category: General
-
Visualising the Colour Cube
The $\text{RGB}$ cube model represents colours as vectors in a three-dimensional vector space, with red, green, and blue as orthogonal basis vectors. A triple $\text{rgb}(r, g, b)$ tells us how far along the red, green, and blue axis our colour is. Pure black is $\text{rgb}(0, 0, 0)$ and pure white is $\text{rgb}(1, 1, 1)$. Two…
-
Homogeneous Coordinate Weirdness
If we plot 4000 points on the line segment from (-1, 0) to (0, 1), and transform each of them with $M = \begin{bmatrix}2 & 3 &4\\-1 & 0 & 0\\2&2&1\end{bmatrix}$, we get an initially surprising result: As we can see, something strange happens in the yellow region of the points. While the red-to-orange points…
-
Silicon Valley’s desperate search for love
Most of [my] work at MIT and before that has been on robotics and autonomous vehicles. But now the dream is to create a system that you can love and that can love you back. Lex Fridman As a fellow computer science student I’m always saddened by Silicon Valley crowd’s desperate quest to find/create love…
-
“Select Next” in MODO and Blender
Comparing “Select Next Active” (Ctrl+Shift+Numpad(+)) in Blender with MODO’s “Select Next” (Arrow Up), MODO very clearly comes out on top. Blender fails to find a plausible next edge to select way too often – even in cases where the next expected edge is quite obvious. This post on the BlenderArtists forums This post on The…
-
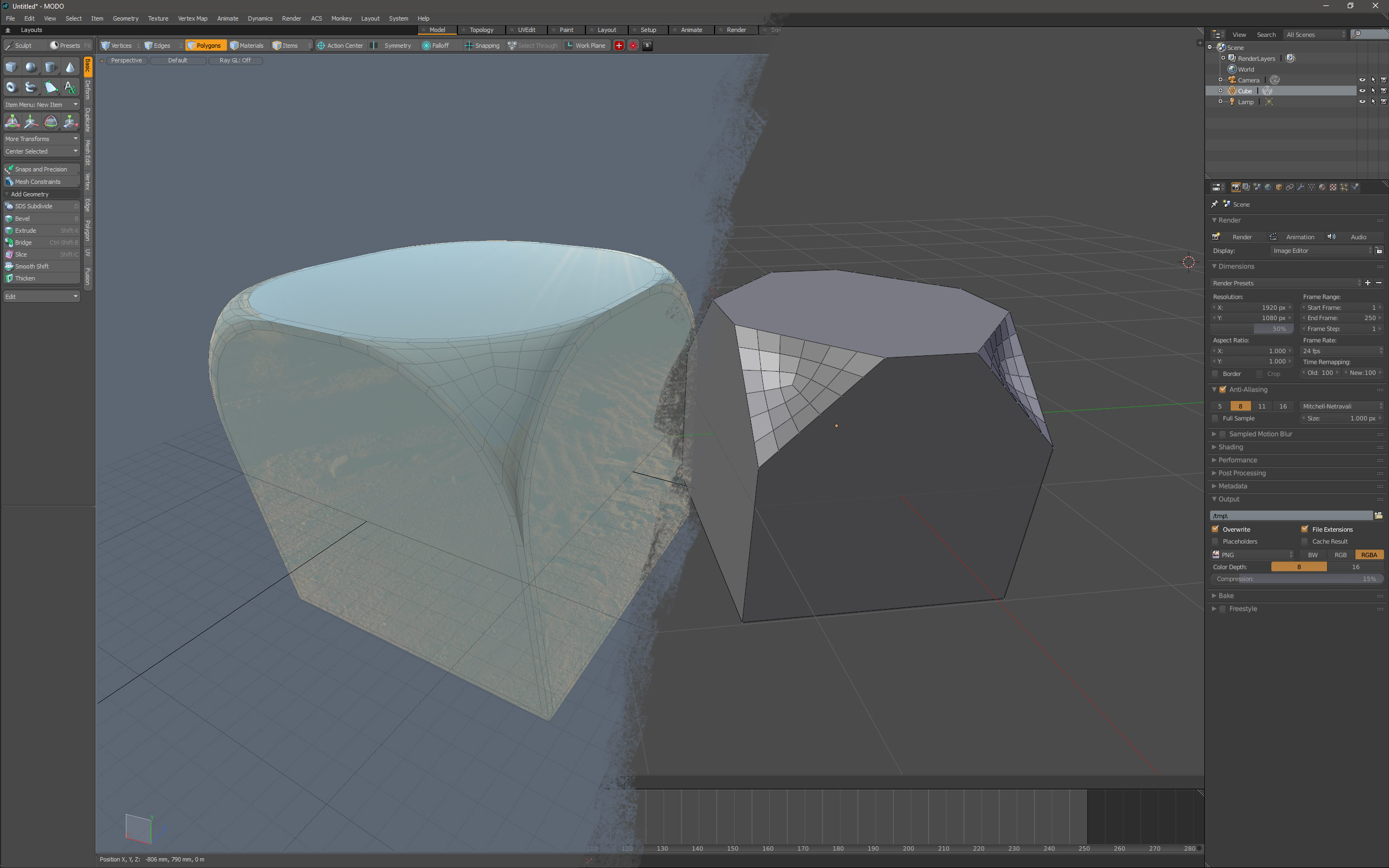
Vertex Bevel Tool in MODO and Blender: Different behaviours but both useful
In the process of comparing basic tools and workflows between MODO and Blender I came across the different behaviours between MODO’s and Blender’s Vertex Bevel tools. In MODO, I get this type of nice rounded effect if I use a Round Level of higher than 0:However, the resulting n-gons surfaces look artifacty unless I then…